

Yesterday, we had an item about how the national polls are sometimes way off, with polling errors between 1% and 7% since 1980. This year, it is a virtual tie nationally and in all the swing states. Nothing seems to move the needle, since Kamala Harris was swapped in as a pinch hitter for Joe Biden:
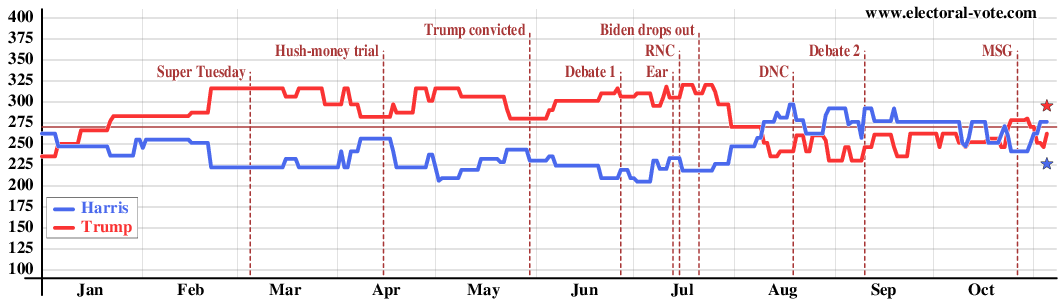
Individual pollsters may have some built-in bias that they don't even know about. Our hope is that by averaging all recent polls, that will cancel out to a large extent. But what if it doesn't? What if, on the whole, the polls are biased a few points one way or another? How much difference would that make?
One way to find out is to conduct a little experiment. To see what would happen if the polls were biased by X points for Harris, we can take all the polling data and subtract X points from Harris and add X points to Donald Trump and see what happens to the electoral vote. Ditto the other way. We did exactly that and here are the results:
| R-5 | R-4 | R-3 | R-2 | R-1 | No error | D-1 | D-2 | D-3 | D-4 | D-5 |
| Trump +160 | Trump +114 | Trump +96 | Trump +86 | Trump +86 | Harris +24 | Harris +45 | Harris +106 | Harris +181 | Harris +271 | Harris +335 |
Here is how to interpret the table. The "No error" column shows the electoral-vote score if the polls are spot-on. This is what today's map shows. But imagine that the pollsters were all underestimating Trump's vote share by 5 points (R-5)—for example, due to "shy Trump voters." This is shown in column 1. Then Trump wins the electoral college by 160 EVs, a huge blowout. Now suppose the pollsters are off by 4 points in Harris' favor. Correcting that gives us column 2 (R-4) in which Trump wins by 114 EVs, and so on. If the polls are off by 1 point in favor of Trump, then correcting that brings us to column 7 (D-1), and Harris wins by 45 EVs. If the polls have missed vast numbers of young voters and Harris does 5 points better than the current polls, she will win by a net margin of 335 EVs.
This model assumes the polls are off the same amount everywhere, which is unlikely. If we tried to compensate for different polling errors in all seven swing states separately, we'd be playing seven-dimensional chess and, we have to admit, we are not so good at that. (V)